Beams and Ornaments

This post describes supplies for the activities in Imago Mobiles and how to prepare them.

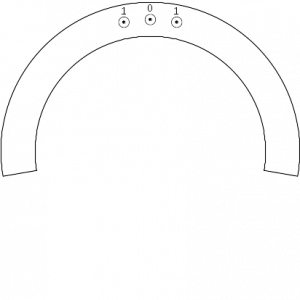
First, you will need straight beams with regularly spaced holes. Ideally the center one will be labeled with a “0”, the two adjacent to the center labeled with “1”s, the next two out labeled with “2”, and so on. You can print out the following PDF, cut out the rectangular beam, and then use a hole punch to make the holes. Be careful to position the holes accurately! Positioning is key to balance.

If you need or want more exactly-constructed beams, you can use the girders from many different construction sets, like Meccano (see for example item #2). Just be sure to use a beam with equally-spaced holes, and an odd number of them, so that there will be a single center hole.

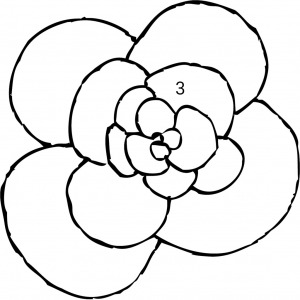
Second, you will need the ornaments. They can really be any objects that you want to hang, with one major proviso: they need to come in a limited number of types, and the weight of the ornaments (including the hooks!) of each type must be identical, and there must be a lightest type, a type that weighs twice as much, a type that weighs three times as much, and so on. Again, for emphasis, those weights should include the weights of the hooks.

Here’s one way to achieve this. Print out five of the caterpillar ornaments below on the heaviest cardstock that will work with your printer. You must use the same weight of cardstock for all ornaments of a given kind. On a very sensitive scale (with 1-gram or better resolution), weigh the five ornaments together. Separately weigh five identical paper clips to use as hooks (you must use all identical paper clips as hooks for all ornaments for this to work!). Divide the measured weights by five to get the weights C of a single caterpillar and P of a single paper clip.

Now make two test copies of the chrysalis (you will be throwing these two out), on the card stock that you want to use for this ornament. Cut them out and weigh them together, dividing the weight by two to get the test weight T of the chrysalis. Then the scaling factor for the final copies of the chrysalis is s = √((2C+P)/T). Calculate the scaling factor, rounding it to the nearest percent. Then print out several copies of the chrysalis, scaling by the computed scaling factor, on the desired card stock. Cut them out, and verify with your scale that a chrysalis with paper clip weighs the same as two caterpillars each with its paper clip.

Follow the same procedure with the flower ornament, except use the formula s = √((3C+2P)/T) for the scaling factor. Verify that one of the scaled flowers with a paper clip weighs the same as three caterpillars with three paper clips. Finally, repeat with the butterfly using the formula s = √((4C+3P)/T) and check that a butterfly with paper clip weighs the same as four caterpillar-paper clip combinations.

Now you have a supply of ornaments for making balanced mobiles. You can twist the paperclips however is helpful for making them into hooks, as long as you don’t break the paperclips or add any tape or anything else that would add weight. You can write down the scaling factor for each ornament, and as long as you use the same paper clips and the same cardstock, you can print and cut out as many ornaments as you like using those scaling factors.

Finally, here are the PDFS for the four types of semicircular beams referred to in the post.