Habito Labyrinth

Nestled in a courtyard of the Divinity School at Southern Methodist University, you will find the Habito Labyrinth. Labyrinths are actually in themselves a subject of study and interest to professional mathematicians, but before we get into that, let’s first ask whether a labyrinth is a maze. That’s of course a matter of terminology, but the key aspect of the passageways that are typically called “labyrinths” is that there are no choices at any point, only a single route that wends its way from the entrance to the center (or exit, depending on the labyrinth). Also typically that path reaches every point within the area comprised by the labyrinth. So there is never any difficulty or strategy in finding your way.

The puzzle, therefore, becomes how to construct a labyrinth — how can you make a pathway that’s guaranteed to reach every point without running into a dead — and how to count how many different labyrinths there are. Those are the places where the mathematics come in.

The study and enjoyment of labyrinths has an extremely ancient history. In fact, here’s a method for constructing a labyrinth hints of which have been found on clay tablets over three thousand years old. Begin with this figure, consisting of a large plus sign, four “L” shapes in the “elbows” of the plus sign, and four dots at the corners. 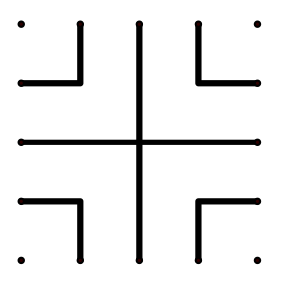The next step is to connect the bottom center point (the end of the bottom branch of the plus sign) to the point immediately to its right (one end of the bottom right “L” shape), like so. Next you connect the point immediately to the left of the ones you just used (one end of the bottom left “L”) to the point immediately to the right of the ones you just used (the bottom right corner point), like so. Now continue in this fashion, always connecting the next unused point to the left around the perimeter of the original diagram to the next unused point to the right, until all of the points have been used and your diagram looks something like this. Now you can trace your way through your labyrinth. There’s an entrance at the top, just to the left of center, and the passages are between the lines you’ve just drawn. You should be able to trace your finger (or other convenient pointer) all the way to the center (where you drew your first arc) without ever retracing your path, and visiting every point enclosed by the outermost arc.

Attached you will find a sheet and directions that will allow you to explore making many more different labyrinths, and you can find lots more information about labyrinths and the mathematics of labyrinths on Prof. Tony Phillips’ website.

LabyrinthDiagram     LabyrinthDirections