Towering Gold

Perhaps the most eye-catching feature of Dallas Fair Park is the gold-leaf wrapped Tower Building. Yes, that is real gold!

Because of the allure and attraction of gold, our first math walk stop in Fair Park will be to ask, “How much is all of that gold on the Tower Building worth?” Before we go through the calculations, stop and take a moment to guess. Is it 1,000 dollars worth of gold if we crumpled it up into a solid nugget of gold? $10,000? A million dollars? Let’s figure it out.

Since gold leaf is gold spread out thinly over an area, we need to figure out the surface area of the building that is covered by gold. We will model the front of the tower as a giant rectangle, the front of the eagle as another rectangle (which is of course a rough approximation, but it’s a small percentage of the entire gold area), and each wing as another rectangle. So we just need the dimensions of each rectangle.

To estimate these dimensions, we can start with the height of the tower from the top of the frieze depicting the history of Texas to the feet of the eagle. We see that it is divided into nine vertical sections that appear to be equal in height. So we will focus on measuring the height of one of these sections, in particular, the bottommost section.

If you stand dead center in front of the building, you will notice as you walk toward the building or away from it that when you are very close to the building, the frieze section appears taller than the first gold section above it, but when you are very far from the building the gold section appears taller. Move back and forth until you get to a spot where the two sections appear to be exactly the same height (lining a pencil up at about arm’s length so that it appears to match one of the sections in height and moving it up and down to compare to the other section can help).

Once you’ve found such a spot, measure the distance to the center of the front wall of the building, and measure the height of the frieze directly with a measuring tape. (I get that the frieze is eleven feet high and that if I stand 22 feet away, the sections appear to be the same height.)

Now take a look at the following diagram — it’s a vertical cross-section of the situation where your eye is at the point marked “I.” 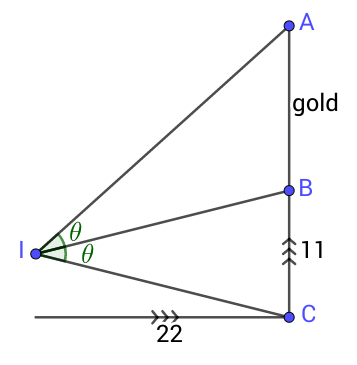The fact that the two sections appear to be the same height means exactly that the two angles labeled theta are the same. Now with just the two dimensions and a little trigonometry, we can figure out the unknown height of the gold section. If you’ve learned some trigonometry, see if you can work it out.

Here’s one way, in which we’ve cut the lower triangle in half with a horizontal line: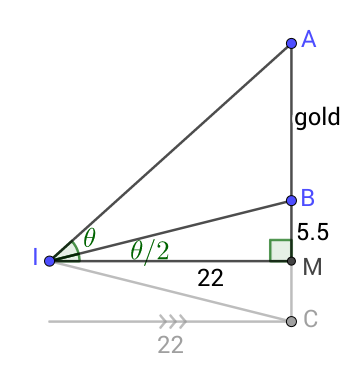

The angle theta/2 has to have tangent 5.5/22 feet, so it is about 14 degrees. Therefore, angle MIA is about 42 degrees, and so leg MA is 22 feet times the tangent of 42 degrees, or about 19.8 feet. Therefore, the gold section BA is 19.8 – 5.5 = 14.3 feet, which we will round to 15 feet for ease of calculation (and because our eyeballing and measuring was very approximate, and the architect was more likely to use round numbers of feet for key measurements of the building).

So the front section of the tower is roughly 9×15=135 feet tall, and we can directly measure how wide it is at the base. I got that it’s about 7 feet wide, but you should make your own measurement.

Now, what about that eagle? We’ll just guess that it’s the same height as one vertical section of the tower; that shouldn’t be too far off. So we’re modeling the front of the eagle as another 15 foot by 7 foot rectangle, and the wings as 15 feet high. So all that remains is the length of the wings, which is the horizontal dimension of the two sides of the tower.

But look closely at the sides of the tower. You will see a faint rectangular grid, with that horizontal dimension three and a half boxes wide. Moreover, two of the boxes side by side appear to form a square! It’s like the builders wrapped the building in graph paper to help us. Therefore, the horizontal dimension we want is 3.5/2 times the height of one vertical section, or about 27 feet.

Adding up all of the sections of gold, there are 135×7 + 15×7 + 15×27 + 15×27 = 1,860 square feet of gold leaf on the building.

How much gold does it take to make 1,860 square feet of gold leaf? Searching the internet, we can find one resource that tells us that 1000 “leaves” of gold cover 79 square feet  and weigh up to 23 grams. Dividing, the 1,860 square feet we need to cover would need 1,860/79 or about 23.5 groups of 1,000 leaves, which would therefore weigh 23.5×23, or about 542 grams.

How much is that much gold worth, if it were crumpled up into one big nugget? To get that answer, we have to convert 542 grams into the unit that gold is bought and sold in: the troy ounce. A troy ounce consists of 31.1 grams, so the gold we’d need to cover the Tower Building would weigh 542/31.1, or approximately 17.43 troy ounces.

To finish off, as of the time of this writing gold has been trading in a range around $1,300 per troy ounce for the past year. Therefore, the raw value of the gold on the Tower building is about 17.43×1,300, or $23,000. Is that more or less than you guessed? If it’s less, then it’s probably because gold leaf is so incredibly thin. By comparison, enough household aluminum foil to cover the Tower Building would weigh about 6,700 grams, or over twelve times as much. Combining that with the fact that gold is over seven times more dense than aluminum tells us that gold leaf is almost 100 times thinner than aluminum foil — yet it’s strong enough to last centuries on the outside of buildings!